Новости
02.07.2020
Книга «Глубокое обучение в картинках. Визуальный гид по искусственному интеллекту»
Джон Крон, Грант Бейлевельд и замечательный иллюстратор Аглаэ Бассенс используют яркие примеры и аналогии, которые позволяют объяснить, что такое глубокое обучение, почему оно пользуется такой популярностью и как эта концепция связана с другими подходами к машинному обучению. Книга идеально подойдет разработчикам, специалистам по обработке данных, исследователям, аналитикам и начинающим программистам, которые хотят применять глубокое обучение в своей работе. Теоретические выкладки прекрасно дополняются прикладным кодом на Python в блокнотах Jupyter. Вы узнаете приемы создания эффективных моделей в TensorFlow и Keras, а также познакомитесь с PyTorch.
Базовые знания о глубоком обучении позволят создавать реальные приложения — от компьютерного зрения и обработки естественного языка до генерации изображений и игровых алгоритмов.
Сеть промежуточной глубины на основе Keras
В завершение этой главы воплотим новые теоретические познания в нейронную сеть и посмотрим, сможем ли мы превзойти предыдущую модель shallow_net_in_keras.ipynb в классификации рукописных цифр.
Первые несколько этапов создания сети промежуточной глубины в блокноте Jupyter intermediate_net_in_keras.ipynb идентичны этапам создания ее предшественницы — неглубокой сети. Сначала загружаются те же самые зависимости Keras, точно так же вносится и обрабатывается набор данных MNIST. Как можно увидеть в листинге 8.1, самое интересное начинается там, где определяется архитектура нейронной сети.
Листинг 8.1. Код, определяющий архитектуру нейронной сети с промежуточной глубиной
 Первая строка в этом фрагменте кода, model = Sequential(), та же, что и в предыдущей сети (листинг 5.6); это экземпляр объекта модели нейронной сети. В следующей строке начинаются расхождения. В ней мы заменили функцию активации sigmoid в первом скрытом слое функцией relu, как было рекомендовано в главе 6. Все остальные параметры первого слоя, кроме функции активации, остались прежними: он все так же состоит из 64 нейронов, и прежней осталась размерность входного слоя — 784 нейрона.
Первая строка в этом фрагменте кода, model = Sequential(), та же, что и в предыдущей сети (листинг 5.6); это экземпляр объекта модели нейронной сети. В следующей строке начинаются расхождения. В ней мы заменили функцию активации sigmoid в первом скрытом слое функцией relu, как было рекомендовано в главе 6. Все остальные параметры первого слоя, кроме функции активации, остались прежними: он все так же состоит из 64 нейронов, и прежней осталась размерность входного слоя — 784 нейрона.
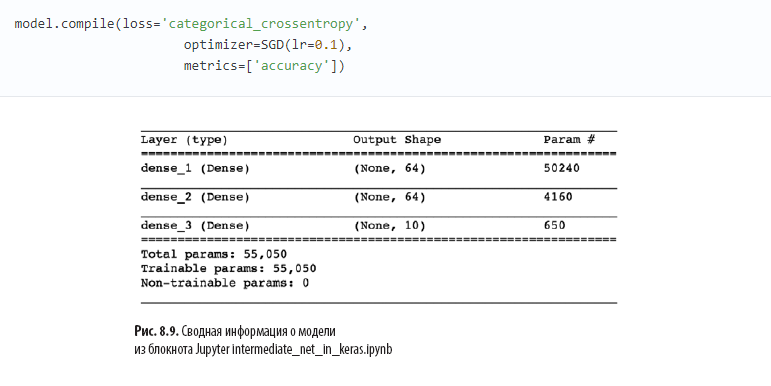
Другое существенное изменение в листинге 8.1 по сравнению с неглубокой архитектурой в листинге 5.6 заключается в наличии второго скрытого слоя искусственных нейронов. Вызовом метода model.add() мы без всяких усилий добавляем второй слой Dense с 64 нейронами relu, оправдывая слово intermediate (промежуточная) в имени блокнота. Вызвав model.summary(), можно увидеть, как показано на рис. 8.9, что этот дополнительный слой добавляет 4160 дополнительных обучаемых параметров, по сравнению с неглубокой архитектурой (см. рис. 7.5). Параметры можно разбить на:
- 4096 весов, соответствующих связям каждого из 64 нейронов во втором скрытом слое с каждым из 64 нейронов в первом скрытом слое (64 × 64 = 4096);
- плюс 64 смещения, по одному для каждого нейрона во втором скрытом слое;
- в результате получается 4160 параметров: nпараметров = nw + nb = 4096 + 64 =
= 4160.
Помимо изменений в архитектуре модели мы также изменили параметры компиляции модели, как показано в листинге 8.2.
Листинг 8.2. Код компиляции нейронной сети с промежуточной глубиной
 Эти строки из листинга 8.2:
Эти строки из листинга 8.2:
- задают функцию стоимости на основе перекрестной энтропии: loss='categorical_crossentropy' (в неглубокой сети использовалась квадратичная стоимость loss='mean_squared_error');
- задают метод стохастического градиентного спуска для минимизации стоимости: optimizer=SGD;
- определяют гиперпараметр скорости обучения: lr=0.1(1);
- указывают, что в дополнение к обратной связи о потерях, которая предлагается библиотекой Keras по умолчанию, мы также хотим получить обратную связь о точности модели: metrics=['accuracy'](2).
(1) Вы можете попробовать увеличить скорость обучения на несколько порядков, а затем уменьшить ее на несколько порядков и понаблюдать, как это повлияет на обучение.
(2) Потеря является наиболее важным показателем, позволяющим увидеть, как изменяется качество модели с течением эпох, но конкретное значение потери зависит от характеристик данной модели и, как правило, не поддается интерпретации и не может сравниваться у разных моделей. Поэтому даже зная, что потери должны быть как можно ближе к нулю, часто очень сложно понять, насколько близка к нулю потеря для конкретной модели. Точность, напротив, легко интерпретируется и легко обобщается: мы точно знаем, что это значит (например, «неглубокая нейронная сеть правильно классифицировала 86 процентов рукописных цифр в проверочном наборе данных»), и можем сравнить с точностью любой другой модели («точность 86 процентов хуже, чем точность нашей глубокой нейронной сети»).
Наконец, мы обучаем промежуточную сеть, выполняя код в листинге 8.3.
Листинг 8.3. Код обучения нейронной сети с промежуточной глубиной

Единственное, что изменилось в обучении промежуточной сети по сравнению с неглубокой сетью (см. листинг 5.7), — это уменьшение на порядок гиперпараметра epochs с 200 до 20. Как вы увидите далее, более эффективная промежуточная архитектура требует намного меньше эпох для обучения.
 На рис. 8.10 представлены результаты первых четырех эпох обучения сети. Как вы наверняка помните, наша неглубокая архитектура достигла плато на уровне 86%-й точности на проверочных данных после 200 эпох. Сеть промежуточной глубины значительно превзошла ее: как показывает поле val_acc, сеть достигла 92.34%-й точности уже после первой эпохи обучения. После третьей эпохи точность превысила 95%, а к 20-й эпохе, похоже, достигла плато на уровне около 97.6%. Мы серьезно продвинулись вперед!
На рис. 8.10 представлены результаты первых четырех эпох обучения сети. Как вы наверняка помните, наша неглубокая архитектура достигла плато на уровне 86%-й точности на проверочных данных после 200 эпох. Сеть промежуточной глубины значительно превзошла ее: как показывает поле val_acc, сеть достигла 92.34%-й точности уже после первой эпохи обучения. После третьей эпохи точность превысила 95%, а к 20-й эпохе, похоже, достигла плато на уровне около 97.6%. Мы серьезно продвинулись вперед!
Разберем подробнее вывод model.fit(), показанный на рис. 8.10:
- Индикатор процесса, показанный ниже, заполняется в течение 469 «циклов обучения» (см. рис. 8.5):
60000/60000 [==============================] - 1s 15us/step означает, что на все 469 циклов обучения в первую эпоху потребовалась 1 секунда, в среднем по 15 микросекунд на цикл.
- loss показывает среднюю стоимость на обучающих данных для эпохи. Для первой эпохи она равна 0.4744 и от эпохи к эпохе уверенно уменьшается методами стохастического градиентного спуска (SGD) и обратного распространения, а в конечном итоге уменьшается до 0.0332 к двадцатой эпохе.
- acc — точность классификации на обучающих данных в данную эпоху. Модель правильно классифицировала 86.37% после первой эпохи и достигла уровня выше 99% к двадцатой. Поскольку модель может переобучиться, не следует особо удивляться высокой точности в этом параметре.
- К счастью, стоимость на проверочном наборе данных (val_loss), как правило, тоже уменьшается и в конечном итоге достигает плато на уровне 0.08 в ходе последних пяти эпох обучения.
- Одновременно с уменьшением стоимости на проверочных данных растет точность (val_acc). Как уже упоминалось, точность на проверочных данных составила 97.6%, что значительно выше 86% у нашей неглубокой сети.
Итоги
В этой главе мы проделали большую работу. Сначала мы узнали, как нейронная сеть с фиксированными параметрами обрабатывает информацию. Затем разобрались с взаимодействующими методами — функциями стоимости, стохастическим градиентным спуском и обратным распространением, которые позволяют корректировать параметры сети для аппроксимации любого истинного значения y, имеющего непрерывное отношение с некоторым входом х. Попутно мы познакомились с несколькими гиперпараметрами, включая скорость обучения, размер пакета и количество эпох обучения, а также с практическими правилами настройки каждого из них. В завершение главы мы применили новые знания для создания нейронной сети промежуточной глубины, которая значительно превзошла предыдущую неглубокую сеть на той же задаче классификации рукописных цифр. Далее мы познакомимся с методами улучшения стабильности искусственных нейронных сетей по мере их углубления, что позволит нам разработать и обучить полновесную модель глубокого обучения.





Комментарии: 0
Пока нет комментариев