Новости
13.10.2020
Книга «Гид по Computer Science для каждого программиста»
Зачем нужна эта книга
Многие из моих(автора) знакомых разработчиков пришли в профессию из самых разных областей. У одних — высшее образование в области Computer Science; другие изучали фотографию, математику или даже не окончили университет.
В последние годы я заметил, что программисты все чаще стремятся изучить Computer Science по ряду причин:
- чтобы стать хорошими программистами;
- чтобы на собеседованиях отвечать на вопросы про алгоритмы;
- чтобы удовлетворить свое любопытство в области Computer Science или наконец перестать сожалеть о том, что в свое время у них не было возможности освоить этот предмет.
Эта книга для всех вас.
Многие найдут здесь темы, интересные сами по себе. Я попытался показать, в каких реальных (неакадемических) ситуациях эти знания будут полезны. Хочу, чтобы, прочитав эту книгу, вы получили такие же знания, как после изучения базового курса по Computer Science, а также научились их применять.
Проще говоря, цель этой книги — помочь вам стать более квалифицированным и опытным программистом благодаря лучшему пониманию Computer Science. Мне не под силу втиснуть в одну книгу 20-летний стаж преподавания в колледже и профессиональный опыт… однако я постараюсь сделать максимум того, на что способен. Надеюсь, что вы найдете здесь хотя бы одну тему, о которой сможете сказать: «Да, теперь мне это понятно», — и применить знания в своей работе.
Чего вы не найдете в издании
Смысл книги состоит в том, чтобы читатель смог лучше понимать Computer Science и применять знания на практике, а вовсе не в том, чтобы полностью заменить четыре года обучения.
В частности, это не книга с доказательствами. Действительно, во втором томе книги рассмотрены методы доказательства, однако стандартные алгоритмы обычно приводятся здесь без доказательств. Идея в том, чтобы читатель узнал о существовании этих алгоритмов и научился их использовать, не вникая в подробности. В качестве книги с доказательствами, написанной для студентов и аспирантов, я настоятельно рекомендую Introduction to Algorithms («Алгоритмы. Вводный курс») Кормена (Cormen), Лейзерсона (Leiserson), Ривеста (Rivest) и Стейна (Stein) (авторов обычно объединяют под аббревиатурой CLRS).
Это и не книга по программированию: вы не найдете здесь рекомендаций, когда использовать числа типа int, а когда — double, или объяснений, что такое цикл. Предполагается, что читатель сможет разобраться в листингах на псевдокоде, используемых для описания алгоритмов (все программы в этой книге написаны на псевдокоде на основе языка С.). Цель книги — связать концепции Computer Science с уже знакомыми читателю методами программирования.
10. Динамическое программирование
10.1. Задача недостающих полей
Предположим, у нас есть шахматная доска размером n × n, на которой недостает нескольких полей. Как найти наибольший участок доски размером k × k без недостающих полей?
Если вы раньше не сталкивались с такой задачей, потратьте несколько минут на то, чтобы написать решение и определить время выполнения вашего алгоритма.
Столкнувшись с этой задачей, я рассуждал следующим образом. Каждое поле шахматной доски может принадлежать ко многим наибольшим участкам, но только в одном из них оно может быть верхним левым углом. Если я помечу каждое поле размером наибольшего неповрежденного участка, верхним левым углом которого он является, то поле с наибольшей такой меткой будет соответствовать искомому участку.
Предположим, что доска представлена в виде матрицы n × n, в которой каждая ячейка содержит 1, если соответствующее поле присутствует, и 0, если оно пропущено. Если текущее значение ячейки равно 0, то соответствующее поле отсутствует и не может быть частью непрерывного участка, поэтому его не нужно изменять. Если же значение равно 1, то мы можем заменить его числом, которое на единицу больше, чем минимальное значение из трех ячеек, расположенных ниже и справа.
Мы изменяем каждую ячейку матрицы один раз, включая проверку, равно ли значение ячейки нулю, проверку значений еще максимум трех ячеек и запись нового значения ячейки. Каждая из этих операций занимает время O(1), поэтому время, необходимое для обработки всей шахматной доски, составляет 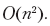
Обратите внимание, что это линейное, а не квадратичное время выполнения алгоритма — на шахматной доске n (мы считаем, что n — это общее количество полей, и придерживаемся обычного соглашения о том, что n — это объем входных данных) полей (некоторые из них отсутствуют), поэтому общее время, затрачиваемое алгоритмом, пропорционально количеству полей. Если более точно обозначить размер шахматной доски как √ n × √ n, то получим n полей и общее время выполнения O(n).
10.2. Работа с перекрывающимися подзадачами
Подход, использованный в этом разделе, называется динамическим программированием. Он применяется, когда задачу можно разделить на несколько подзадач, решение каждой из которых будет использовано несколько раз. Этот подход отличается от принципа «разделяй и властвуй», когда задачу разделяют на подзадачи, которые решаются независимо друг от друга. В задаче с шахматной доской каждая подзадача зависела от решений трех других задач, а решения всех подзадач сохранялись для дальнейшего использования.
Динамическое программирование обычно выполняется путем построения таблиц, как показано выше. Это означает решение задачи методом «снизу вверх», когда мы начинаем с решения наименьших подзадач и продвигаемся вверх до тех пор, пока не придем к ответу. Другой метод — это мемоизация, при которой мы идем сверху вниз, решая подзадачи по мере необходимости и кэшируя результаты для повторного использования. Построение таблиц — предпочтительный вариант, когда нужно решить каждую подзадачу (в моем примере с шахматной доской нужно было найти наибольший неповрежденный участок для каждого поля доски), поскольку затраты у этого метода меньше, чем при мемоизации. Если некоторые подзадачи из области решения не обязательно решать, то мемоизация позволяет решать только те подзадачи, которые действительно необходимы.

Ключевой момент
Там, где метод «разделяй и властвуй» подразумевает разделение задачи на несколько независимых подзадач, динамическое программирование подразумевает разделение задачи на несколько перекрывающихся подзадач. Решение каждой подзадачи кэшируется для последующего повторного использования.
10.3. Динамическое программирование и кратчайшие пути
Рассмотрим задачу поиска кратчайшего пути: для заданного графа со взвешенными ребрами нужно найти такой путь из одного узла в другой, который имеет наименьшую стоимость.
Определение
Граф со взвешенными ребрами — это граф, в котором каждое ребро имеет свой вес (стоимость). Стоимость пути из одного узла в другой определяется суммой стоимости всех пройденных ребер.
Предположим, что мы нашли путь между узлами s и t, который содержит третий узел v. Тогда путь из s в t должен содержать кратчайший путь из s в v, поскольку в противном случае мы могли бы заменить этот участок более коротким путем и уменьшить длину кратчайшего пути из s в t, что противоречит начальному условию (это принцип оптимальности Беллмана).
Ключевой момент
Динамическое программирование (и жадные алгоритмы) полезно для решения задач, имеющих оптимальную подструктуру. Это означает, что оптимальное решение задачи может быть эффективно построено из оптимальных решений ее подзадач. Если самый короткий путь из Мэдисона в Денвер проходит через Омаху, то этот маршрут также должен содержать самый короткий путь из Мэдисона в Омаху и из Омахи в Денвер.
Если задача имеет и оптимальную подструктуру, и перекрывающиеся подзадачи, то она становится кандидатом на решение методом динамического программирования.
Задачи поиска кратчайшего пути представляют собой яркие примеры динамического программирования, поскольку оптимальное свойство подструктуры интуитивно понятно — очевидно, что самый быстрый способ перехода из точки А в точку С через точку В — это также самый быстрый способ перехода из точки А в точку В и из точки В в точку С. В число алгоритмов, основанных на этом принципе, входит метод Беллмана — Форда, который находит кратчайший путь из исходной точки в любую вершину графа (или от любой вершины графа до конечной точки) и метод Флойда — Уоршелла — с его помощью вычисляется кратчайший путь между каждой парой вершин графа. В обоих случаях идея состоит в том, чтобы начать с небольшого подмножества узлов, близких к интересующим нас узлам, и постепенно расширять это множество, используя уже найденные узлы для вычисления новых расстояний.
10.4. Примеры практического применения
10.4.1. Git merge
Еще одна задача, на примере которой обычно демонстрируют возможности динамического программирования, — поиск наибольшей общей подпоследовательности (Longest Common Subsequence). Задача состоит в том, чтобы для двух заданных строк A и B найти самую длинную последовательность, которая встречается в обеих строках с сохранением последовательности символов. Символы в строках не обязательно должны стоять подряд; например, если A = {acdbef} и B = {babdef}, то {adef} будет их общей подпоследовательностью.
При слиянии изменений в Git (merge) выполняется поиск наибольшей общей подпоследовательности для master и рабочей веток. Символы, присутствующие в master, но отсутствующие в наибольшей общей подпоследовательности, удаляются; символы, которые есть в рабочей ветке, но отсутствуют в этой подпоследовательности, добавляются в master.
10.4.2. LATEX
Систему подготовки документов LATEX часто используют для создания технических документов. Одна из задач системы набора текста — выравнивание текста одновременно по правому и левому краю; для этого интервалы между словами и символами растягиваются или сжимаются таким образом, чтобы все строки имели одинаковую длину. Другой способ выровнять текст состоит в переносе последнего слова, так что часть слова оказывается в следующей строке. LATEX (С технической точки зрения практически всю работу выполняет система ввода текста TEX; LATEX построена на основе TEX. Здесь я использую LATEX из соображений простоты) пытается найти оптимальные точки разрыва строки, чтобы текст выглядел красиво. Если это сделать не удастся, то несколько строк подряд будут заканчиваться переносом слова или же расстояние между словами в разных строках будет различаться. В LATEX существует набор правил для оценки «неудачности» выравнивания. Программа стремится найти «наименее плохой» вариант.
Если в абзаце есть n возможных точек разрыва строки, то существует 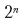 возможных вариантов разбиения текста. «Неудачность» выбора для каждой точки разрыва зависит от того, какие точки разрыва были выбраны до нее. Следовательно, у нас снова есть перекрывающиеся подзадачи. Использование методов динамического программирования сокращает время выполнения до
возможных вариантов разбиения текста. «Неудачность» выбора для каждой точки разрыва зависит от того, какие точки разрыва были выбраны до нее. Следовательно, у нас снова есть перекрывающиеся подзадачи. Использование методов динамического программирования сокращает время выполнения до 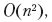 которое может быть улучшено с помощью дополнительных методов.
которое может быть улучшено с помощью дополнительных методов.





Комментарии: 0
Пока нет комментариев